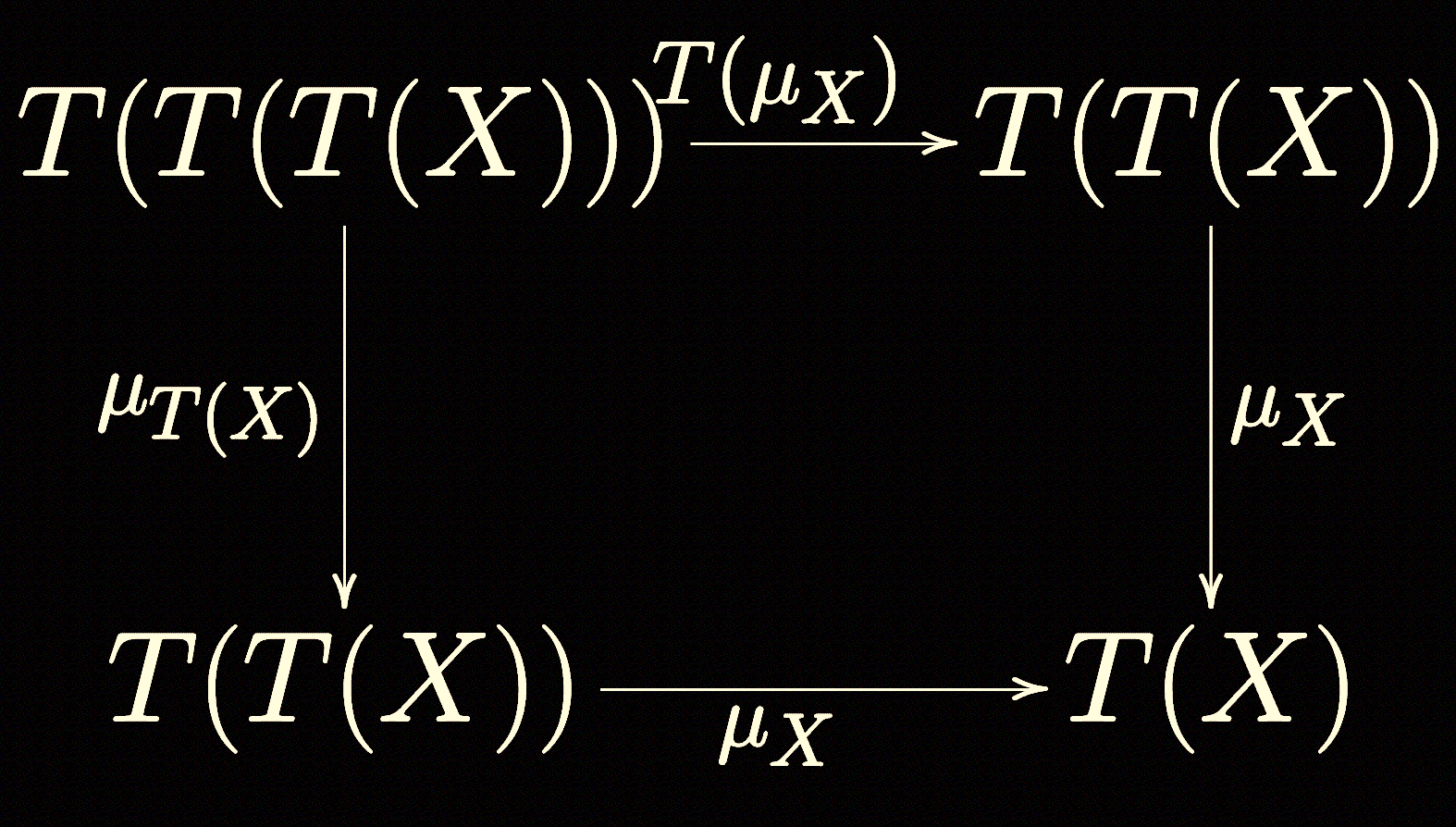Scala and Category Theory 2

I'm interested in the more category-theoretic aspects of functional programming. To this end, I have been working towards an elevator pitch on category theory for Scala devs (or alternatively, an elevator pitch on Scala for mathematicians). This is part 2.

Recap of Functors

Any parameterized type with a map method is a functor, more or less.

Recap of Natural Transformations

A map between two functors. I.e. if F[] and G[] are parameterized types with map methods, then we have a function eta(A): F[A] => G[A] for every type A. This must commute with the map methods for F and G.

Adjunctions in the Scala Category

There are three ways of identifying two functors as being inverse to each other. They are summarized in the following table.

Isomorphism in this context literally means an isomorphism in the category of categories. Equivalence means that $FG$ (respectively $GF$) is isomorphic to the identity in the functor category. Isomorphism and equivalence are too restrictive to be ubiquitous, so category theorists prefer to talk about adjunctions instead.

An adjunction can be equivalently defined as a pair of functors, $F:\mathscr{C}\to\mathscr{D}$ and $G:\mathscr{D}\to\mathscr{C}$, for which there are natural isomorphisms

for all $A\in\mathscr{C}$ and $B\in \mathscr{D}$. One canonical example of an adjunction is the Hom-product adjunction

which shows up everywhere in mathematics. In the Scala category, the hom-product adjunction is known as currying. That is, an identification between the types (A, B) => C and A => (B => C).

Unit and Co-Unit of the Currying Adjunction

The canonical maps $\eta:\text{id}_{\mathscr{C}} \to GF$ and $\epsilon:FG \to \text{id}_{\mathscr{D}}$ are called the unit and co-unit of the adjunction, respectively.

type Product[B] = (B, A)
type Id[B] = B

object ProdFunctor extends Functor[Product] {
  // Unfortunate failure in scala destructuring functionality.
  def fmap[X, Y](f: X => Y): Product[X] => Product[Y] = { case (x: X, a: A) =>
    (f(x), a)
  }
}

object IdFunctor extends Functor[Id] {
  def fmap[X, Y](f: X => Y): Id[X] => Id[Y] = f
}

type ProdHom[B] = Product[CovariantHom[B]]
object ProdHomFunctor extends Functor[ProdHom] {
  def fmap[X, Y](
      f: X => Y
  ): Product[CovariantHom[X]] => Product[CovariantHom[Y]] =
    (ProdFunctor
      .fmap[CovariantHom[X], CovariantHom[Y]](_))
      .compose(HomFunctor.fmap[X, Y])(f)
}

type HomProd[B] = CovariantHom[Product[B]]
object HomProdFunctor extends Functor[HomProd] {
  def fmap[X, Y](
      f: X => Y
  ): CovariantHom[Product[X]] => CovariantHom[Product[Y]] =
    (HomFunctor
      .fmap[Product[X], Product[Y]](_))
      .compose(ProdFunctor.fmap[X, Y])(f)
}

object CurryingUnit extends NaturalTransformation[Id, HomProd] {
  def etaMapObs[B]: Id[B] => CovariantHom[Product[B]] = (b: B) =>
    (a: A) => (b, a)
}

object CurryingCoUnit extends NaturalTransformation[ProdHom, Id] {
  def etaMapObs[B]: Product[CovariantHom[B]] => Id[B] = { case (f, a) =>
    f(a)
  }
}

Motivation for Monads

Suppose I want to duplicate every item in an array. I have a function

def f[A](x: A): List[A] = List(x, x)

If I map f over List(1, 2, 3), then I obtain

List(1, 2, 3).map(f) == List(List(1, 1), List(2, 2), List(3, 3))

In order to obtain the correct result, I need to call flatten on the right hand side. Or do it in one call with flatMap, but that is behaviorally identical to calling map and then flatten. The point is that map and flatten are two methods in a trait that must be implemented for this sort of computation.

Properties for a Monad

Such a design pattern as that satisfied by List (i.e., implementing map and flatten with some as-yet-undiscussed compatibility axioms) is actually what is known as a Monad.

The map method is inherited from the fact that a monad is a functor, while the flatten method is one of two natural transformations that must be defined alongside the functor.

Some Exmaples

Unsurprisingly, most of the obvious functors in functional programming are actually monads. This includes List, Option, and Promise (almost). The monad construction allows for very generic program design and algebraic debugging. Here is the definition.

type Id[A] = A

object IdFunctor extends Functor[Id] {
  def fmap[X,Y](f: X => Y) = f
}

trait Monad[F[_]] extends Functor[F[_]] {
  object fflatten extends NaturalTransformation[F[F[_]], F[_]]

  object unit extends NaturalTransformation[Id[_], F[_]]
}